Battery Management Systems
Lithium-ion battery usage has matured into a prevalent element of contemporary electronic technologies, enveloping industries such as mobile computing and electric vehicle development. Cells of this chemistry provide a high energy density, combined with minimal self-discharge, making them ideal candidates for use in technology as production costs decline. An increase in efficacy and severity of operating cycles dictates a need for better predictive and observing capabilities of the cells. Some modern implementations have fallen short, however, requiring consumer batteries to be sold with a surplus energy capacity on the order of 20% to 50%, negating many of the advantages of the battery's chemistry, with respect to weight, and subsequent cost. In order to overcome this overdesign, a focus has been placed on battery management, particularly examining state and parameter estimation, for the purposes of higher fidelity predictive models, leading to informed control schema that result in longer cyclic operational periods and overall lifespan.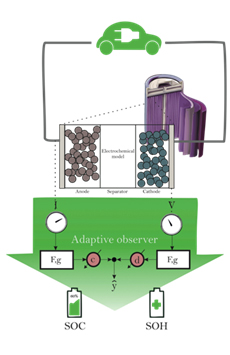
The imperative for an effective battery management system (BMS) is driven by the need to determine two metrics of the lifecycle of a battery, ensuring safe operation and optimal performance through informed control mechanisms. Specifically, the measurement of the state of charge (SOC) and the state of health (SOH) drive the effective control of a cell charge cycle. While conceptually simple and intuitively related to the condition of a battery, the necessary values required to calculate these metrics are not directly attainable outside of a laboratory setting. This drives the need for simultaneous state and parameter estimation, relying solely on the outputs of voltage and temperature, as well as the input current, to determine the full manifestation of a cell.
The SOC of a cell is an instantaneous snapshot of the intercalated lithium in the solid electrode normalized by the maximum capacity of the solid at a given point within that solid, defined as local utilization. The bulk SOC can then be described as the average local utilization with respect to a specific volume, namely the anode or cathode. Given the duration of a single charge cycle of a battery, this metric is a fast changing state that cannot be measured directly in situ, driving the need for accurate state estimation from a given input current and measured output voltage. If the SOC is underestimated, the capacity of a cell is underutilized, while if the SOC is overestimated, the cell can be discharged past its safe limit. This motivates the need for accurate estimation of the internal states of a battery, for the purpose of cost reduction and safe operation.
Unlike the SOC, the SOH of a cell is a long term metric describing the degradation of physical parameters within the cell. Commonly, this metric is binned into two causations, in the form of capacity fade and the increase of impedance due to the ohmic internal resistance of the battery. Charge capacity fade is typified by a decrease in energy over long timelines, for example, the nominal capacity of a cell decreasing by 25% after two years of use. Impedance increase reduces the available power discharge, manifesting in some cases as a 20% reduction in nameplate power availability. As these parameters change, the performance of the battery can be negatively affected, especially without a cognizant awareness of their progression. Additionally, at some point, this degradation becomes untenable, and a cell must be recycled. Without a way of estimating the SOH, this point is based on the intuition of users, without quantitatively informed encouragement, leading to frustration with a product or the potential for unacceptably fast discharge cycles.
To ensure the safe operation of a cell, accurate determinations of the SOC, as well as the SOH, are needed. In this project, we propose the use of a reduced order model that preserves the dominant electrochemical features as well as the simultaneous estimation of states and parameters using an adaptive observer. Once the underlying parameters, as well as the SOC and SOH, are estimated, these estimates can be used to determine a suitable control strategy. The task of this controller is to ensure that the cell is neither charged nor discharged past its limits.
Low Order, High Fidelity Battery Models
A prerequisite for improving cell performance through control solutions is a high fidelity battery model. Widely used in the field, an analytical model known as the Doyle-Fuller-Newman Model, or DFN model, using porous electrode theory, is the basis for many simulation formulations. This model is represented through several partial differential equations and an algebraic constraint, and while consistent in its accuracy, belies a simplicity necessary for battery management in its computational complexity. Moreover, control-oriented models, with a reduction of computed states, are critical in the evolution of the field, and one such model, known as the Single Particle Model, goes to great lengths to correct this problem but lacks the ability to accurately represent the electrochemical dynamics of high discharges. Additionally, research has focused on extending this model to more adequately incorporate these dynamics, and model order reduction techniques have been applied to ensure acceptable simulation performance for use with parameter estimation.
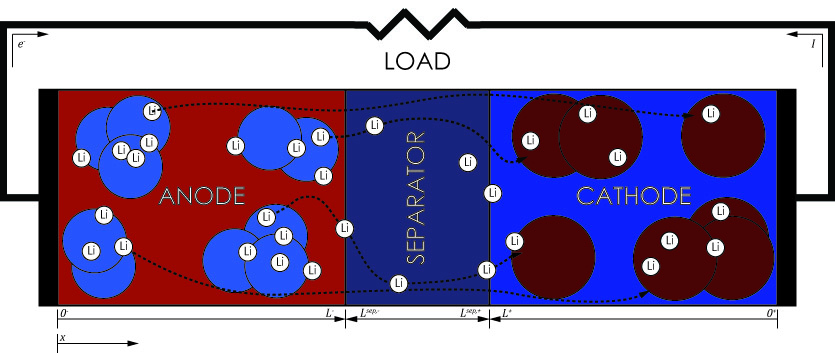 The DFN analytical model combines a series of PDE equations coupled by an algebraic expression defined by the Butler-Volmer reaction kinetics. The model, also commonly referred to as the pseudo two dimensional (P2D) model, disregards any variation in reaction dynamics along non-dominant dimensions, thus normalizing inputs, and considers only one dominant direction, along the x-axis. Along this dimension, the electrode volumes are discretized into spherical solids, with radial dimension, r. A diagram of a cell is shown to the right.
The DFN analytical model combines a series of PDE equations coupled by an algebraic expression defined by the Butler-Volmer reaction kinetics. The model, also commonly referred to as the pseudo two dimensional (P2D) model, disregards any variation in reaction dynamics along non-dominant dimensions, thus normalizing inputs, and considers only one dominant direction, along the x-axis. Along this dimension, the electrode volumes are discretized into spherical solids, with radial dimension, r. A diagram of a cell is shown to the right.
ANCF
An alternative model currently under development at AACL is able to incorporate a lofty charge and discharge rate using elements constructed from the mathematical description of highly flexible beam elements, entitled the Absolute Nodal Coordinate Formulation, or ANCF. By using this nodal polynomial representation, the electrochemical dynamics of the cell are able to be represented by a lesser number of states, ideal for estimation of the cell, while physical parameters are maintained.
The ANCF lithium ion model is capable of achieving high energy discharge simulation results, with minimal states. Using a mathematical basis originally intended for highly flexible beam analysis, the high order variation of internal dynamics within the solid electrode and electrolyte can be captured, while also using a reduced number of states compared to the full order DFN. A volume averaged projection is incorporated to solve the PDE within the electrode, while the Galerkin method is used to solve the dynamic effects of the electrolyte. Finally, orthogonal collocation, using Gauss-Legendre quadrature, is used to solve the DAE constraints of the molar flux. This provides the full model necessary to fulfill the needs of the modern battery management system.
ANCF-e
The main idea of ANCF model is to use a polynomial-basis function to reduce the underlying PDE to an ODE, resulting in much fewer states than in DFN, but in a significantly more accurate performance compared to SPM. One of the main limitations of ANCF, however, is the construction of an ODE approximation of the underlying molar flux, j (x, t), at each instant t, which is governed by the underlying algebraic constraints due to the Butler-Volmer kinetics. The structure of the polynomial basis function introduces high degrees of freedom which in turn leads to poorly conditioned numerical constraints in the molar flux, j(x, t). This is a key point, as the accuracy of the model is dependent on accurate results of the flux constraint, and as such, the ANCF-model poses a significant computational burden. This in turn limits its use for observer design and therefore any real-time parameter estimation that is observer- based. The ANCF-e model that we propose in this paper seeks to overcome this disadvantage by using two sets of basis functions, where the first is based on the polynomial basis function as in the ANCF model and is used to derive an accurate set of electrolyte dynamics, while the second is based on a linear basis function, so as to enable a computable approximation to the molar flux. This in turn is used to synthesize an overall observer that can identify the parameters of the linear dynamics.
Adaptive observers using the ANCF-e model
Several challenges arise in the construction of adaptive observers using the ANCF-e model. The model includes fairly complex spatio-temporal relations between inputs, states, and outputs, compounded by the presence of multiple nonlinearities related to various potentials. This prevents a straight forward application of standard tools of parameter estimation and adaptive observers, both linear and nonlinear. A new approach has been developed to overcome this difficulty which consists of grouping the overall model into four subsystems, where each subsystem is amenable to the development of real-time parameter estimation. Adaptive observers are constructed for the parameter estimation of concentration dynamics through extensions of the state-of-the-art in adaptive observers, including (a) results of an observer that combines spatial and time filtered regressor signals, leveraging shared parameters for each half-cell; and (b) a new Jacobian-based adaptive observer structure, allowing learning to progress in an unknown parameter manifold.
Machine Learning subsystem in the ANCF-e model
The results of the adaptive observers in ANCF-e model however made some assumptions related to inputs and outputs of the underlying nonlinearities, which we will relax in this paper. In particular, the ANCF-e model was broken down into four subsystems, three of which were linear and dynamic, and the fourth was nonlinear. The nonlinear subsystem is fairly complex in nature, and relates the underlying states of the dynamic system to three potentials, such as the electrolyte potential, open-circuit potential, and over-potential, all of which together contribute to the output voltage. An assumption was made that these dynamic states are available at each instant of time, which in turn was crucial in order to carry out real-time parameter estimation of the dynamic subsystems. However, this assumption is reasonable only if one can estimate each of the three underlying potentials. Given that the relationships between the states and potentials are nonlinear, such an estimation can be carried out effectively using a machine learning approach such as neural networks.
A radial basis function based neural network with three layers was chosen as the basis of the machine learning subsystem. The outputs of the neural network are selected carefully as independent ratios of the potentials, which are less dynamic and better distributed compared with potentials themselves. An appropriate dataset of inputs and outputs in the cell is collected for training and testing purposes. Battery simulation tests and suitable pre-processing were carried out while assembling the dataset. The training algorithms of the RBF neural network includes clustering algorithms, standard regression method and further fine-tuning, which makes use of the Gradient Descent Back-propagation (GDB) algorithm as well as the pseudo-inverse (PI) method. The feasibility and accuracy of the proposed machine learning subsystem is demonstrated through numerical validations with different battery conditions and working profiles.
Matrix Regressor Adaptive Observers
Alongside the development of the ANCF model is the generation of tools to solve the SOC/SOH estimation problem for battery management systems using fast state estimation and parameter identification algorithms. Leveraging the structure of the SPM and ANCF model which include linear dynamics as well as static nonlinearities on output and feedthrough channels, adaptive observers are being adapted to handle these nonlinearities while preserving the dynamics in their linear form.
To overcome the slow estimation and adaptation of the original adaptive observer algorithms of the 80's, a new Matrix Regressor (MR) based adaptive observer was introduced by the AAC lab for purposes of battery estimation. Rather than generating additional regressor vectors through successive filtering of the input signal, unique filters are used which halves the number of integrators any signal is exposed to in the overall observer. These MR adaptive observers allow a simple relationship between the degree of persistent excitation and the rate of convergence to be derived, which can then used to optimize the design of the external signal for arbitrarily fast convergence. The notion of strong persistent excitation is introduced, which enables an online computation of the degree of persistent excitation as well as exponential, not only asymptotic, stability.